FOLHA ENEM 2020 - CADERNO 4 - MATEMÁTICA

CADERNO DE QUESTÕES 4 - MATEMÁTICA (ctrl+p para imprimir)

1. (Colégio Marista)

Alguns medicamentos podem ser administrados na forma de solução, medida prática para crianças ou pessoas com dificuldade de engolir pílulas e comprimidos. Assim, um tratamento pode ser realizado por meio de doses de determinada solução, em vez de comprimidos.

Um médico prescreve a um paciente a ingestão de 10 gotas de medicamento na forma de solução, duas vezes ao dia, por 30 dias seguidos. Esse medicamento pode ser comprado sob encomenda, em frascos preenchidos com a quantidade mais próxima do prescrito, em mútiplos de 10ml.

Considerando como regra que cada mililitro de solução equivale a 25 gotas, o volume a ser prescrito pelo médico, de acordo com a situação descrita, deve ser:

a) 20 ml

b) 24ml

c) 30ml

d) 500ml

e) 600ml

2. (Colégio Marista)

Um posto de coleta de sangue organizou informações sobre os doadores durante determinada hora, como mostra tabela a seguir:

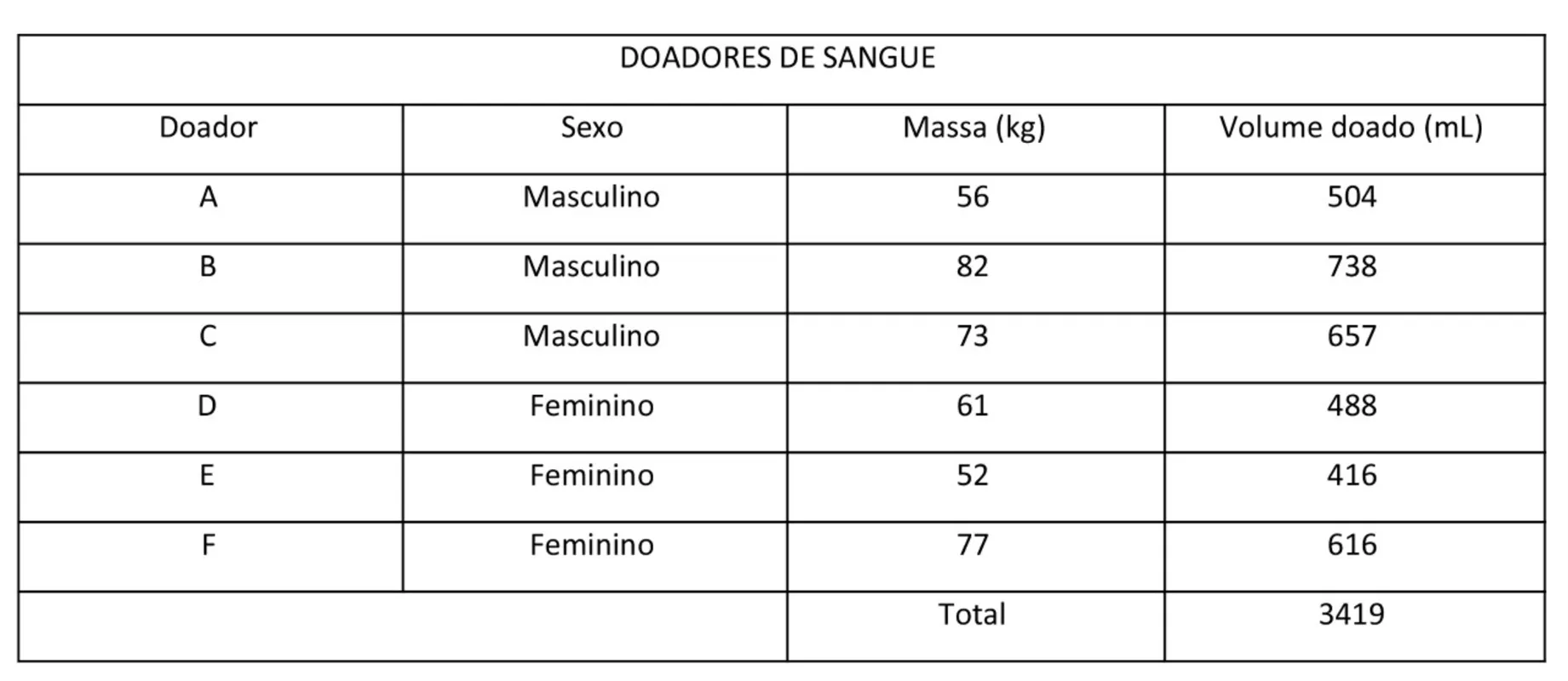
Considerando os dados mostrados na tabela, a relação entre o volume de sangue doado e a massa do doador é de proporção:

a) Direta, com 9mL/kg para ambos os sexos.

b) Inversa, com 8,5mL/kg para ambos os sexos.

c) Direta, com 9mL/kg para o sexo masculino e 8mL/kg para o sexo feminino

d) Direta, com 8mL/kg para o sexo masculino e 9mL/kg para o sexo feminino.

e) Inversa, com 9mL/kg para o sexo masculino e 8mL/kg para o sexo feminino.

3. (Colégio Marista)

No dia 09 de outubro é comemorado o Dia Nacional do Livro. Isto porque nesta data, em 1810, foi criada a Fundação Biblioteca Nacional, existente até os dias atuais no Rio de Janeiro. É a mais antiga instituição cultural brasileira, com um acervo de aproximadamente 9,2 milhões de itens, dos quais 2,5 milhões também podem ser acessados pela internet, através da Biblioteca Digital.

A parte do acervo da Fundação que pode ser acessada na internet corresponde aproximadamente a :

a) 4%

b) 21%

c) 79%

d) 37%

e) 27%

4. (Colégio Marista)

A imagem a seguir representa o rótulo destacado de um pote de mel de abelhas que, planificado, tem o formato de um retângulo de medidas 22cm X 5cm.

Esse rótulo fica enrolado na parte cilíndrica de secção circular do pote. Quando fixado ao pote, há um apequena sobreposição de 1cm sobre si mesmo nas extremidades menores, onde é passada a cola que mantém fixo.

Considerando a aproximação de π = 3, o diâmetro do pote de mel é:

a) 7,0 cm

b) 3,7 cm

c) 3,5 cm

d) 7,3 cm

e) 7,7 cm

5. (Colégio Marista)

A imagem a seguir representa uma chave de campeonato de futebol em sua fase eliminatória.

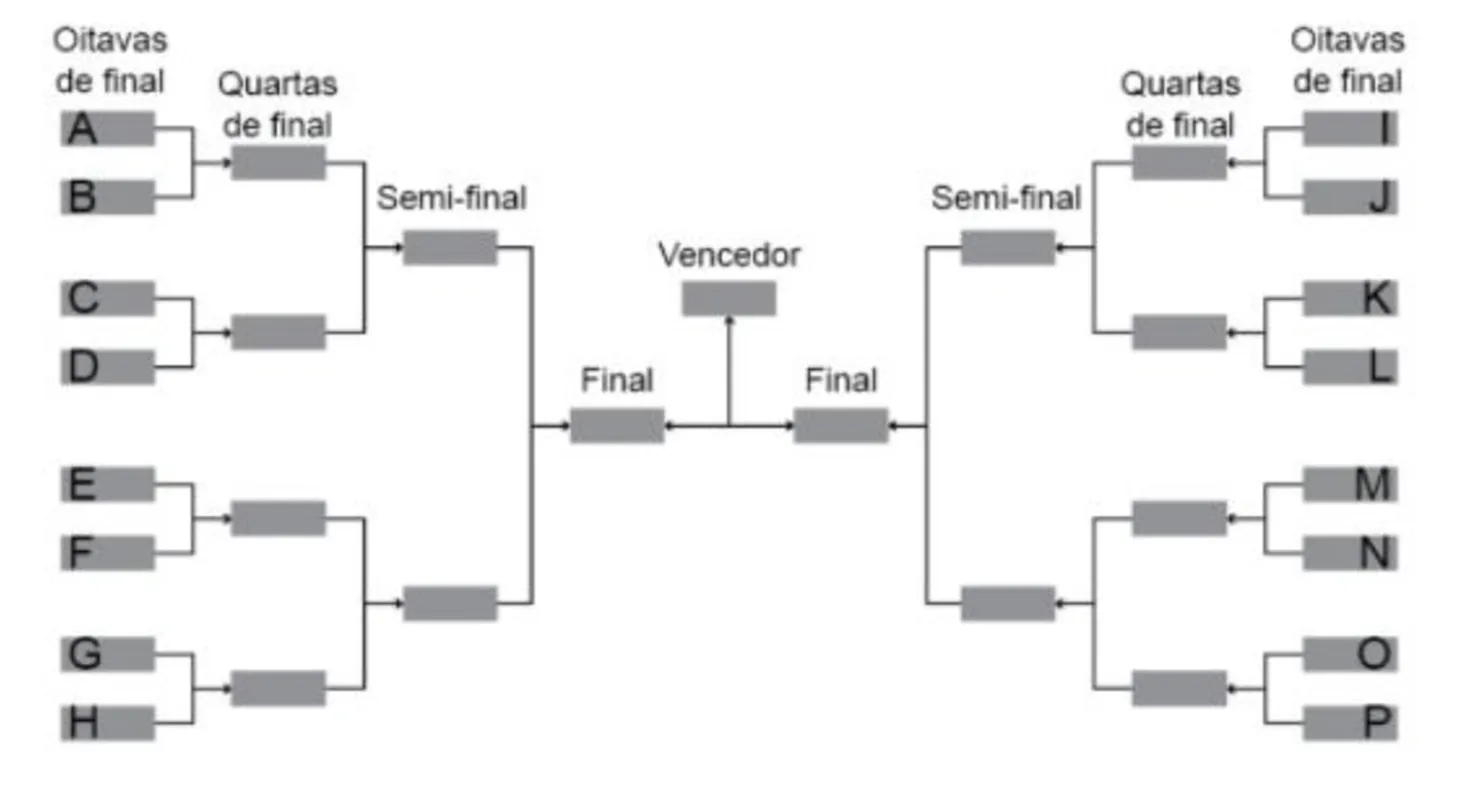
Levando em consideração que uma equipe deve vencer cada partida (não pode haver empates), qual dos possíveis cenários não pode acontecer no final do campeonato?

a) A contra N.

b) J contra O.

c) C contra L.

d) H contra J.

e) E contra P.

6. (Colégio Marista)

Matrioska é um brinquedo tradicional da Rússia, também conhecido como boneca russa. É formada por várias bonecas, costumeiramente feitas de madeira, e que se encaixam umas dentro das outras. Para que isso seja possível, todas possuem o mesmo formato, com variações de tamanho. A pintura decorativa deve ser personalizada.

A Matrioska representada na figura tem seis peças, com alturas a partir da peça maior, de 15 cm, 13 cm, 11 cm e 9 cm.

Mantendo essa sequência, as alturas das peças menores deve ser:

a) 5cm e 3cm.

b) 6cm e 3cm.

c) 7cm e 5cm.

d) 7cm e 6cm.

e) 8cm e 7cm.

7. (Colégio Marista)

O Banco Central do Brasil possui um ranking de reclamações contra instituições financeiras. Para tanto, o Banco calcula um indicador chamado índice, dado pela razão entre o número de reclamações recebidas e o número de clientes de cada instituição multiplicada por 1000 000. O ranking é feito por ordem decrescente do índice.

Considere três instituições financeiras, cujas reclamações e números de clientes estão dispostos na tabela.

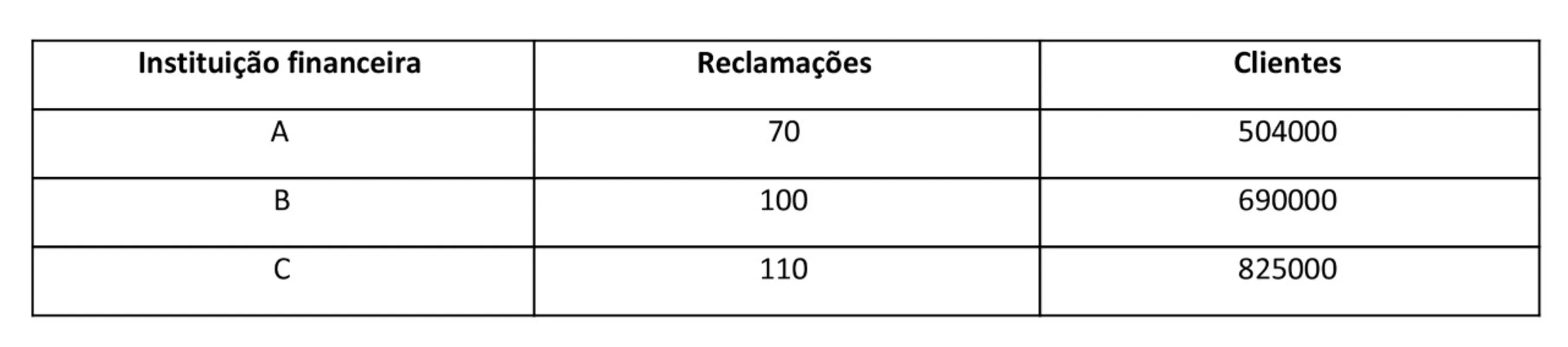
Nesta situação, o ranking será

a) B, A, C.

b) A, B, C.

c) C, A, B.

d) B, C, A.

e) C, B, A.

8. (Colégio Marista)

Um empresário quer instalar aquecedores no seu salão de beleza para melhorar o conforto e seus clientes no inverno. Ele estuda a compra de dois tipos de aquecedores: um modelo A, que consome 600g/h (gramas por hora) de gás propano e cobre 35m2, ou modelo B, que consome 750g/h de gás propano e cobre 45 m2 de área. O fabricante indica que o aquecedor deve ser instalado em um ambiente com área menor do que a sua cobertura. O empresário vai instalar uma unidade por ambiente e quer gastar o mínimo de gás possível, A área do salão a ser climatizada encontra-se na planta (ambiente representado por três retângulos e um trapézio)

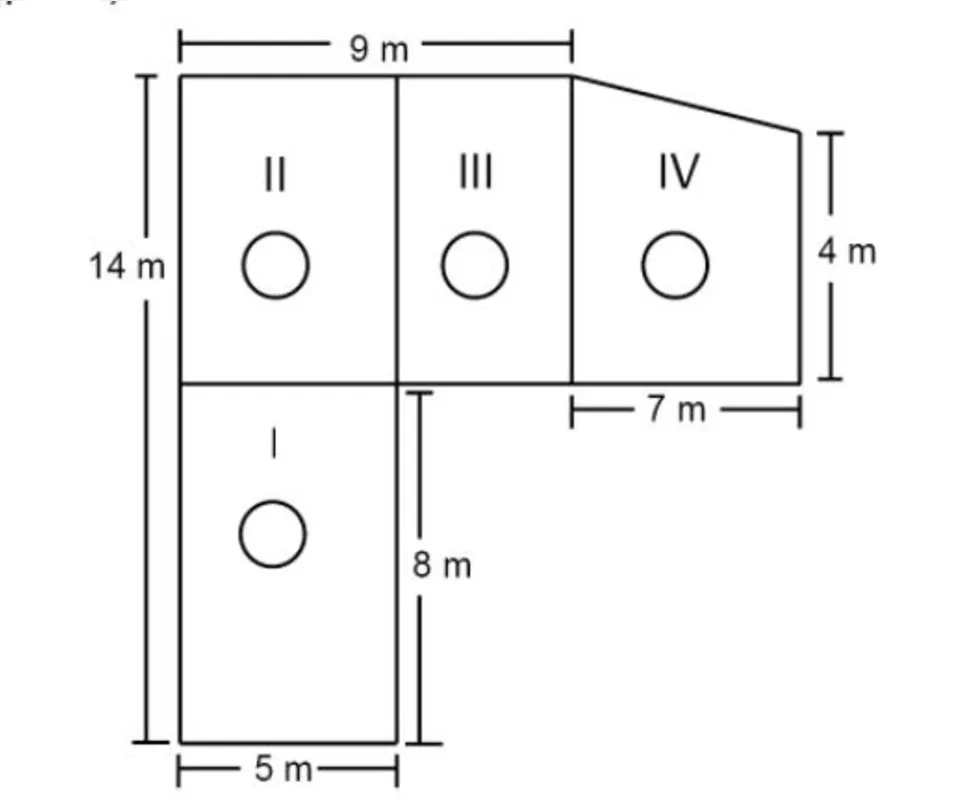
Avaliando-se todas as informações, serão necessários:

a) Quatro unidades do tipo A e nenhuma unidade do tipo B.

b) três unidades do tipo A e uma unidade do tipo B.

c) duas unidades do tipo A e duas unidades do tipo B.

d) uma unidade do tipo A e três unidades do tipo B.

e) nenhuma unidade do tipo A e quatro unidades do tipo B.

9. (ENEM)

Para criar um logotipo, um profissional da área de design gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.

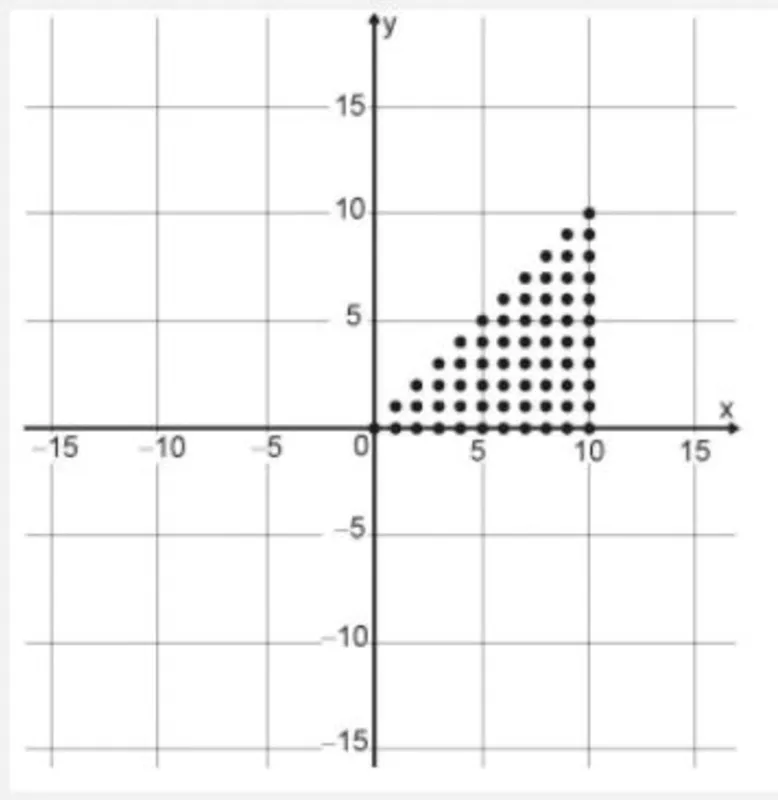
Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.

a) 0 ≤ y ≤ x ≤ 10

b) 0 ≤ x ≤ y ≤ 10

c) 0 ≤ x ≤ 10,0 ≤ y ≤ 10

d) 0 ≤ x+y ≤ 10

e) 0 ≤ x+y ≤ 20

10. (ENEM)

A figura mostra uma praça circular que contém um chafariz em seu centro e, em seu entorno, um passeio. Os círculos que definem a praça e o chafariz são concêntricos.

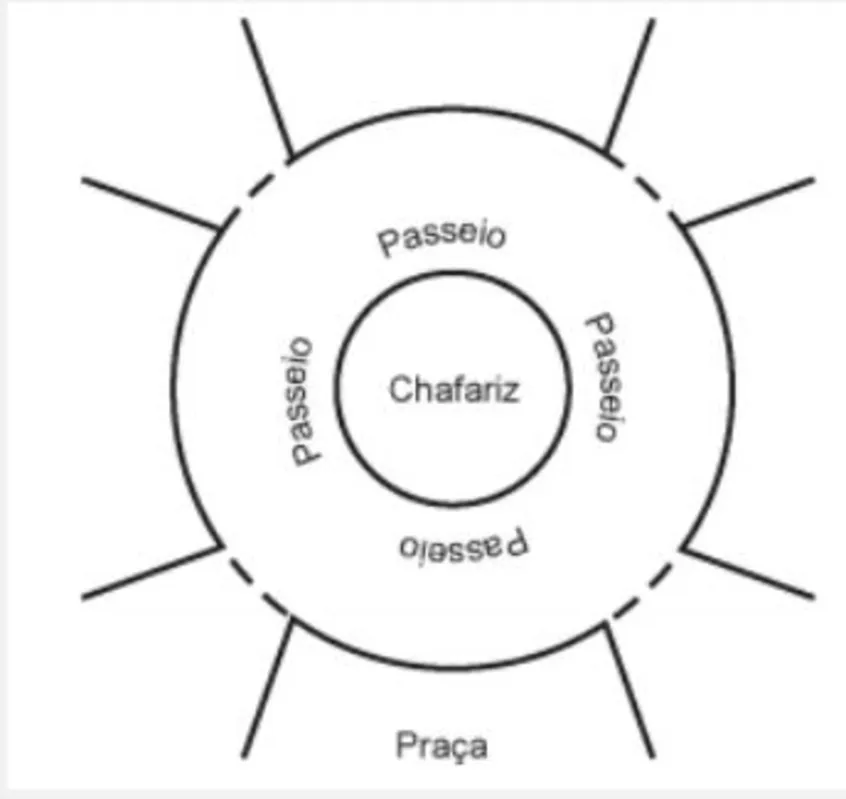
O passeio terá seu piso revestido com ladrilhos. Sem condições de calcular os raios, pois o chafariz está cheio, um engenheiro fez a seguinte medição: esticou uma trena tangente ao chafariz, medindo a distância entre dois pontos A e B, conforme a figura. Com isso, obteve a medida do segmento de reta AB: 16 m.

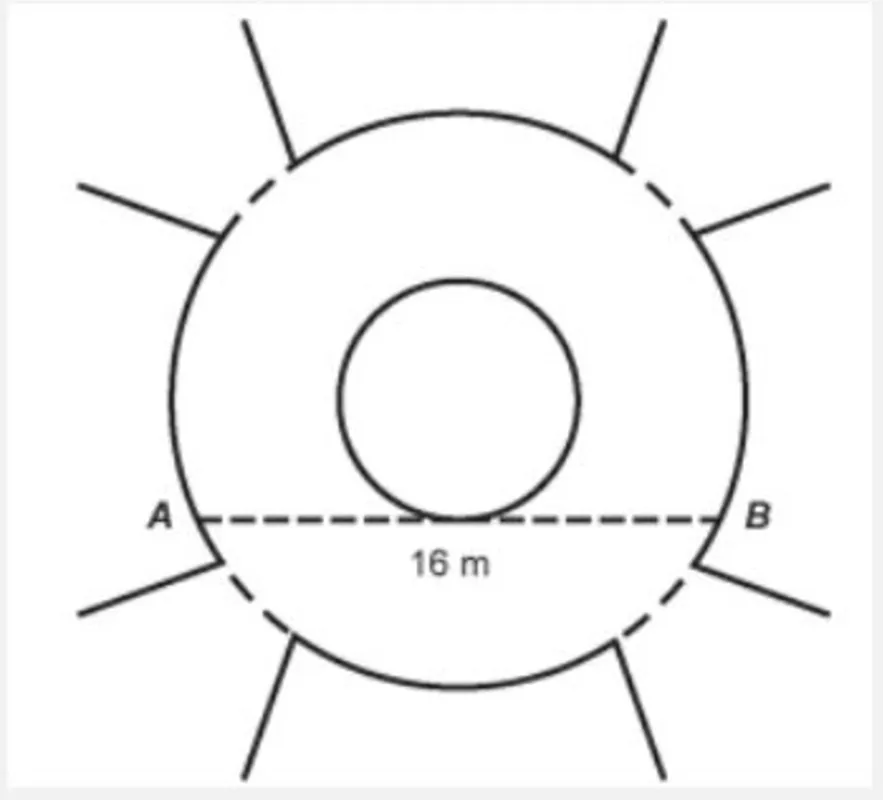
Dispondo apenas dessa medida, o engenheiro calculou corretamente a medida da área do passeio, em metro quadrado.

a) 4 π

b) 8 π

c) 48 π

d) 64 π

e) 192 π

11. (ENEM)

O remo de assento deslizante é um esporte que faz uso de um barco e dois remos do mesmo tamanho. A figura mostra uma das posições de uma técnica chamada afastamento.

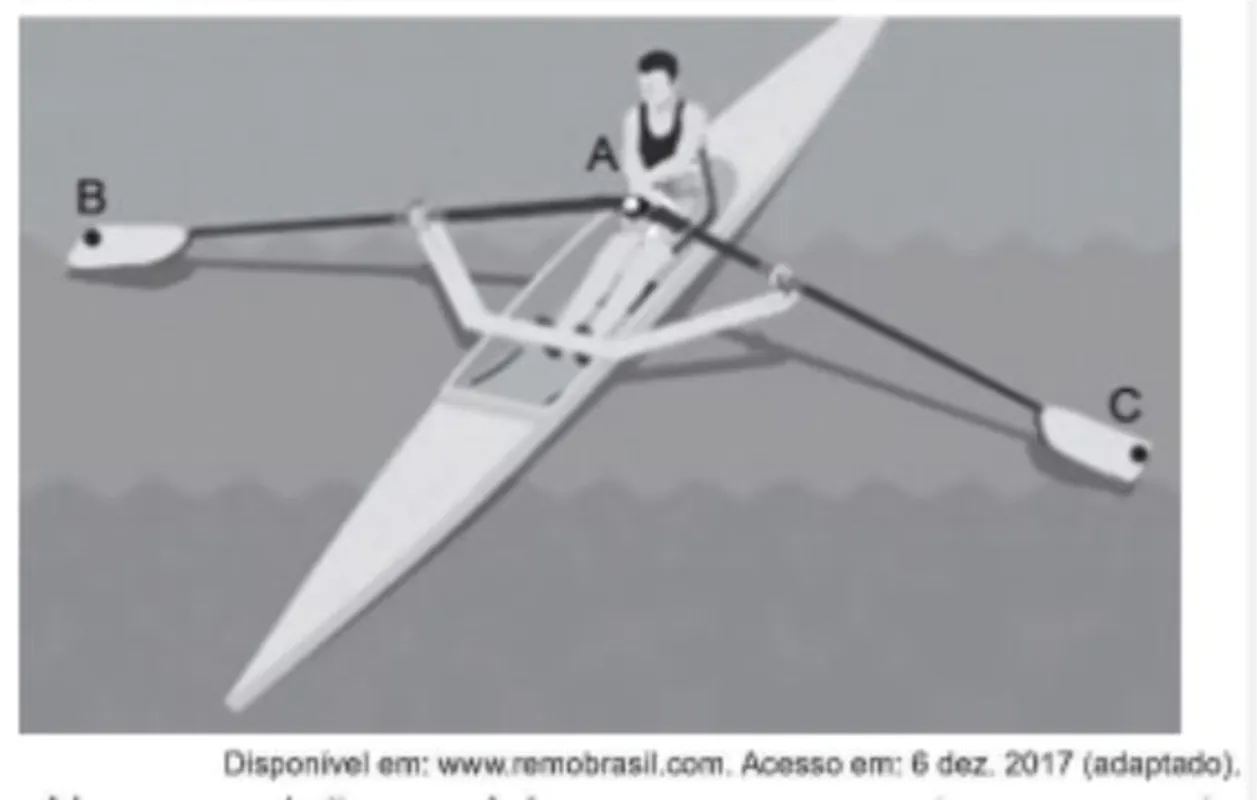
Nessa posição, os dois remos se encontram no ponto A e suas outras extremidades estão indicadas pelos pontos B e C. Esses três pontos formam um triângulo ABC cujo ângulo BÂC tem medida de 170°.

O tipo de triângulo com vértices nos pontos A, B e C, no momento em que o remador está nessa posição, é:

a) Retângulo escaleno

b) Acutângulo escaleno

c) Acutângulo isósceles.

d) Obtusângulo escaleno.

e) Obtusângulo isósceles.

12. (ENEM)

Um rapaz estuda em uma escola que fica longe de sua casa, e por isso precisa utilizar o transporte público. Como é muito observador, todos os dias ele anota a hora exata (sem considerar os segundos) em que o ônibus passa pelo ponto de espera. Também notou que nunca consegue chegar ao ponto de ônibus antes de 6h 15 min da manhã. Analisando os dados coletados durante o mês de fevereiro, o qual teve 21 dias letivos, ele concluiu que 6 h 21 min foi o que mais se repetiu, e que a mediana do conjunto de dados é 6 h 22 min.

A probabilidade de que, em algum dos dias letivos de fevereiro, esse rapaz tenha apanhado o ônibus antes de 6 h 21 min da manhã é, no máximo:

a) 4/21

b) 5/21

c) 6/21

d) 7/21

e) 8/21

13. (ENEM)

Um mapa é a representação reduzida e simplificada de uma localidade. Essa redução, que é feita com o uso de uma escala, mantém a proporção do espaço representado em relação ao espaço real. Certo mapa tem escala 1 : 58 000 000.

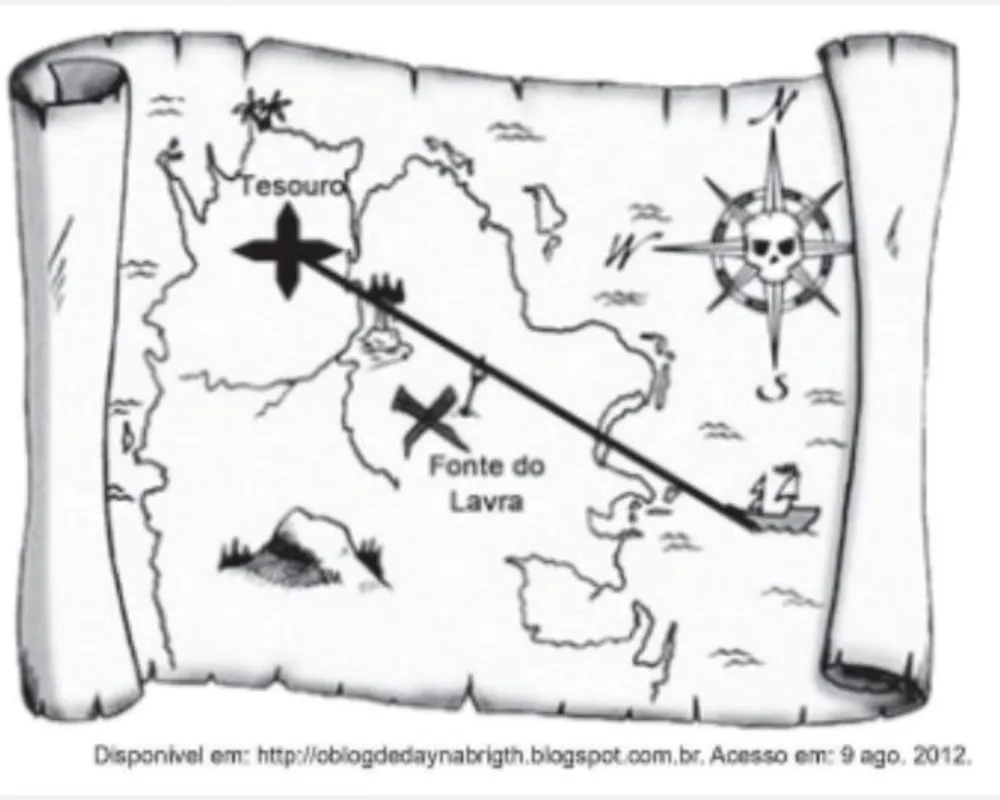
Considere que, nesse mapa, o segmento de reta que liga o navio à marca do tesouro meça 7,6 cm.

A medida real, em quilômetro, desse segmento de reta é

a) 4408

b) 7632

c) 44080

d) 76316

e) 440800

14. (ENEM)

Um produtor de milho utiliza uma área de 160 hectares para as suas atividades agrícolas. Essa área é dividida em duas partes: uma de 40 hectares, com maior produtividade, e outra, de 120 hectares, com menor produtividade. A produtividade é dada pela razão entre a produção, em tonelada, e a área cultivada. Sabe-se que a área de 40 hectares tem produtividade igual a 2,5 vezes à da outra. Esse fazendeiro pretende aumentar sua produção total em 15%, aumentando o tamanho da sua propriedade. Para tanto, pretende comprar uma parte de uma fazenda vizinha, que possui a mesma produtividade da parte de 120 hectares de suas terras.

Qual a área mínima, em hectare, que o produtor precisará comprar?

a) 36

b) 33

c) 27

d) 24

e) 21

15. (ENEM)

Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, de temperatura menos elevada.

Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é:

a) 30

b) 40

c) 45

d) 60

e) 68

16. (ENEM)

Torneios de tênis, em geral, são disputados em sistema de eliminatória simples. Nesse sistema, são disputadas partidas entre dois competidores, com a eliminação do perdedor e promoção do vencedor para a fase seguinte. Dessa forma, se na 1ª fase o torneio conta com 2n competidores, então na 2ª fase restarão n competidores, e assim sucessivamente até a partida final. Em um torneio de tênis, disputado nesse sistema, participam 128 tenistas.

Para se definir o campeão desse torneio, o número de partidas necessárias é dado por:

a) 2 X 128

b) 64 + 32 + 16 + 8 + 4 + 2

c) 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1

d) 128 + 64 + 32 + 16 + 8 + 4 + 2

e) 64 + 32 + 16 + 8+ 4 + 2+ 1

17. (ENEM)

O artigo 33 da lei brasileira sobre drogas prevê a pena de reclusão de 5 a 15 anos para qualquer pessoa que seja condenada por tráfico ilícito ou produção não autorizada de drogas. Entretanto, caso o condenado seja réu primário, com bons antecedentes criminais, essa pena pode sofrer uma redução de um sexto a dois terços.Suponha que um réu primário, com bons antecedentes criminais, foi condenado pelo artigo 33 da lei brasileira sobre drogas.

Após o benefício da redução de pena, sua pena poderá variar de

a) 1 ano e 8 meses a 12 anos e 6 meses.

b) 1 ano e 8 meses a 5 anos.

c) 3 anos e 4 meses a 10 anos.

d) 4 anos e 2 meses a 5 anos.

e) 4 anos e 2 meses a 12 anos e 6 meses.

18. (ENEM)

Um edifício tem a numeração dos andares iniciando no térreo (T), e continuando com primeiro, segundo, terceiro, …, até o último andar. Uma criança entrou no elevador e, tocando no painel, seguiu uma sequência de andares, parando, abrindo e fechando a porta em diversos andares. A partir de onde entrou a criança, o elevador subiu sete andares, em seguida desceu dez, desceu mais treze, subiu nove, desceu quatro e parou no quinto andar, finalizando a sequência. Considere que, no trajeto seguido pela criança, o elevador parou uma vez no último andar do edifício.

De acordo com as informações dadas, o último andar do edifício é o:

a) 16º

b) 22º

c) 23º

d) 25º

e) 32º

ACESSE TAMBÉM:

FOLHA ENEM:

FOLHA ENEM - Provas de ciências da natureza e a atenção ao invisível

FOLHA ENEM 2020 - CADERNO 3 - CIÊNCIAS DA NATUREZA

Os quatro elementos e invenções históricas ainda têm espaço no Enem

ESPECIAL ENEM 2020- História e geografia são carro-chefe na prova de ciências humanas

ENEM 2020 - Ministério da Justiça monta sistema de acompanhamento do Enem

FOLHA ENEM | Caderno 2 - Ciências Humanas

FOLHA ENEM | Gabarito - Caderno 2 - Ciências Humanas

ENEM 2020: Candidatos devem estar antenados ao que acontece no Brasil e no mundo

SIMULADO ENEM| Uma ajuda especial da FOLHA e Colégio Marista para as provas do Enem 2020

FOLHA ENEM | Caderno 1 - Linguagens e Códigos

FOLHA ENEM | Gabarito - Linguagens e Códigos

HORA DE ESTUDAR! Folha de Londrina lança caderno especial com questões e conteúdos exclusivos para o Enem 2020