FOLHA ENEM 2023 - CADERNO 14

CADERNO 14

MATEMÁTICA E SUAS TECNOLOGIAS

01. (ENEM)

A receita R de uma empresa ao final de um mês é o dinheiro captado com a venda de mercadorias ou com a prestação de serviços nesse mês, e a despesa D é todo o dinheiro utilizado para pagamento de salários, contas de água e luz, impostos, entre outros. O lucro mensal obtido ao final do mês é a diferença entre a receita e a despesa registradas no mês. O gráfico apresenta as receitas e despesas, em milhão de real, de uma empresa ao final dos cinco primeiros meses de um dado ano.

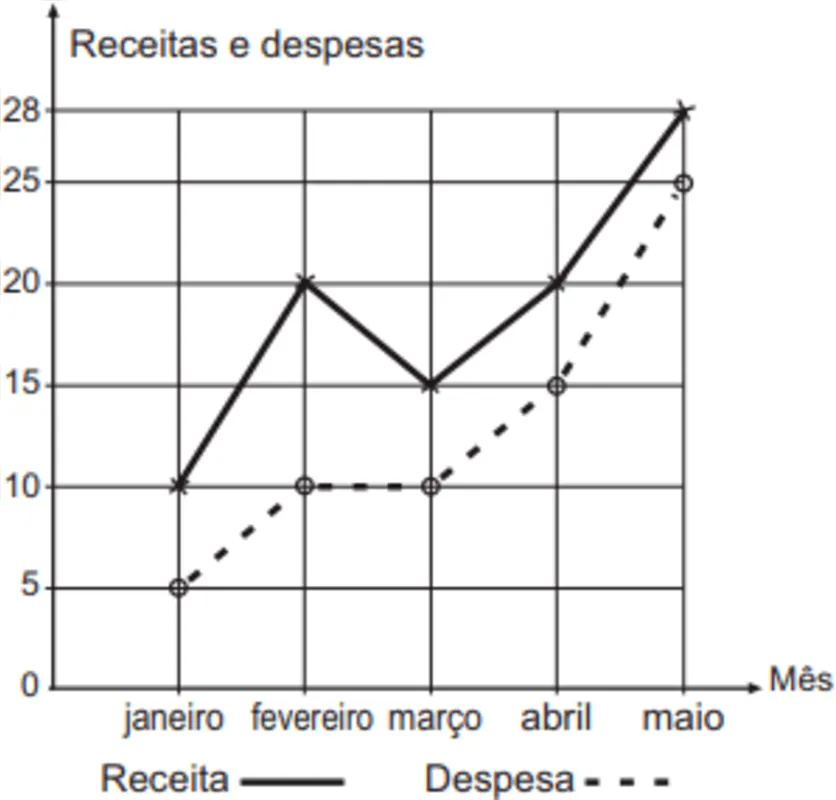
A previsão para os próximos meses é que o lucro mensal não seja inferior ao maior lucro obtido até o mês de maio.

Nessas condições, o lucro mensal para os próximos meses deve ser maior ou igual ao do mês de

a) janeiro.

b) fevereiro

c) março.

d) abril.

e) maio.

02. (ENEM)

Uma pessoa realizou uma pesquisa com alguns alunos de uma escola, coletando suas idades, e organizou esses dados no gráfico.

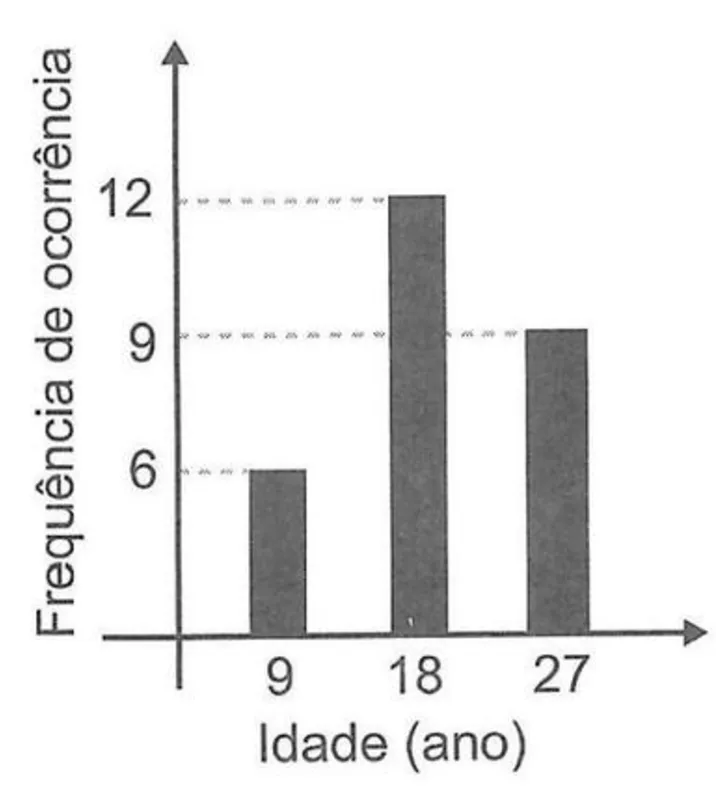
Qual é a média das idades, em ano, desses alunos?

a) 9

b)12

c)18

d) 19

e) 27

03. (ENEM)

Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é completamente reabastecido por carros-pipa.

Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π.

Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a

a) 1,12.

b) 3,10.

c) 4,35.

d) 4,48

e) 5,60.

04. (ENEM)

O quadro apresenta o número de terremotos de magnitude maior ou igual a 7, na escala Richter, ocorridos em nosso planeta nos anos de 2000 a 2011.

Um pesquisador acredita que a mediana representa bem o número anual típico de terremotos em um período.

Segundo esse pesquisador, o número anual típico de terremotos de magnitude maior ou igual a 7 é

a) 11.

b) 15.

c) 15,5

d 15,7.

e) 17,5.

05. (ENEM)

Uma grande rede de supermercados adota um sistema de avaliação dos faturamentos de suas filiais, considerando a média de faturamento mensal em milhão. A matriz da rede paga uma comissão para os representantes dos supermercados que atingirem uma média de faturamento mensal (M), conforme apresentado no quadro.

Um supermercado da rede obteve os faturamentos num dado ano, conforme apresentado no quadro.

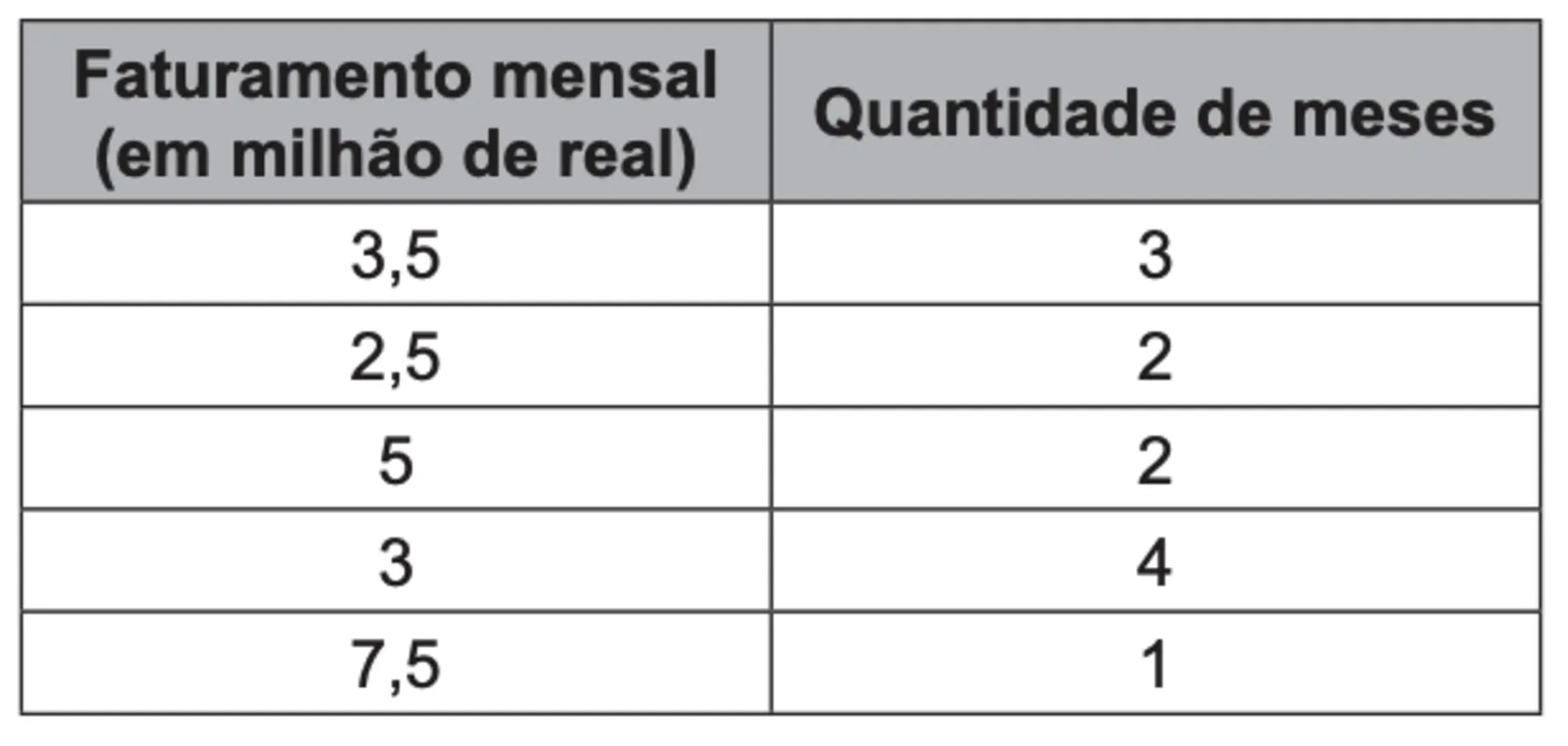
Nas condições apresentadas, os representantes desse supermercado avaliam que receberão, no ano seguinte, a comissão de tipo

a) I.

b) II.

c) III.

d) IV.

e) V.

06. (ENEM)

Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

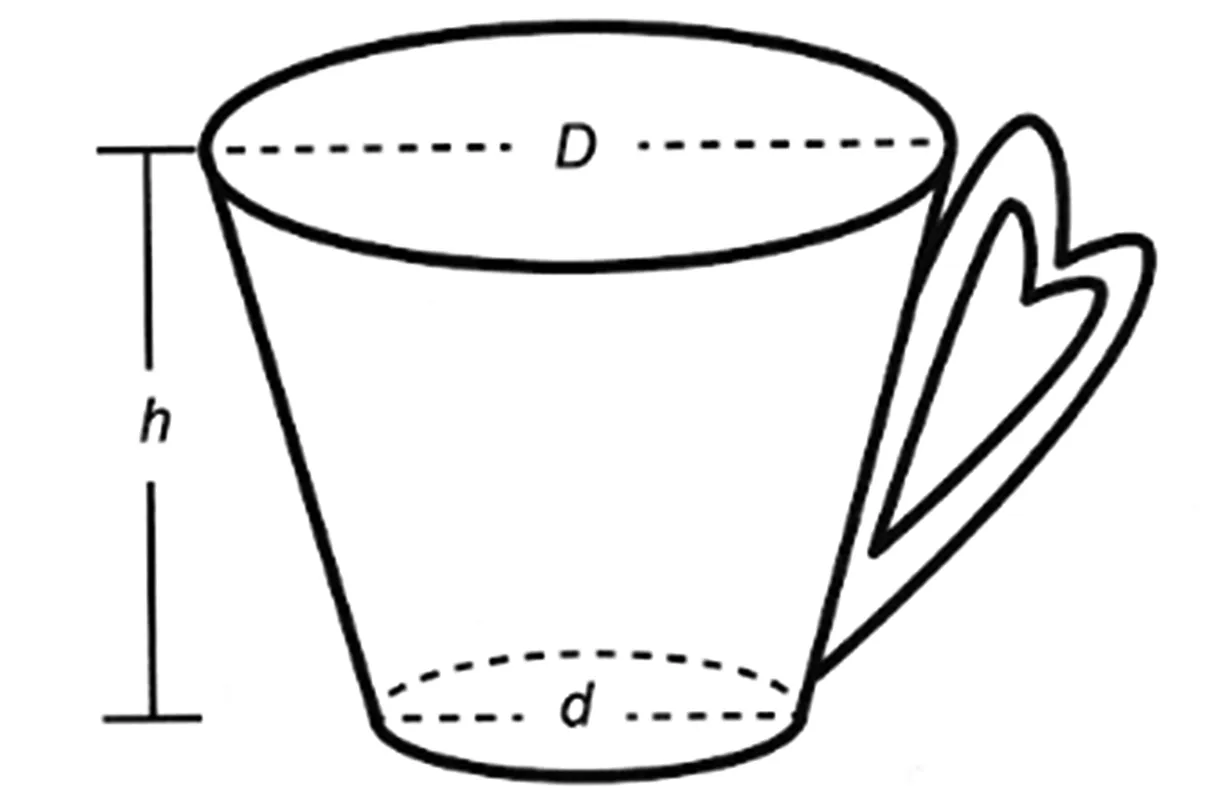
Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).

Utilize 3 como aproximação para π.

Qual é a capacidade volumétrica, em mililitro, dessa caneca?

a) 216

b) 408

c) 732

d) 2 196

e) 2 928

07. (ENEM)

Uma rede de hamburgueria tem três franquias em cidades distintas. Visando incluir um novo tipo de lanche no cardápio, o gerente de marketing da rede sugeriu que fossem colocados à venda cinco novos tipos de lanche, em edições especiais. Os lanches foram oferecidos pelo mesmo período de tempo em todos os franqueados. O tipo que apresentasse a maior média por franquia seria incluído definitivamente no cardápio. Terminado o período de experiência, a gerência recebeu um relatório descrevendo as quantidades vendidas, em unidade, de cada um dos cinco tipos de lanche nas três franquias.

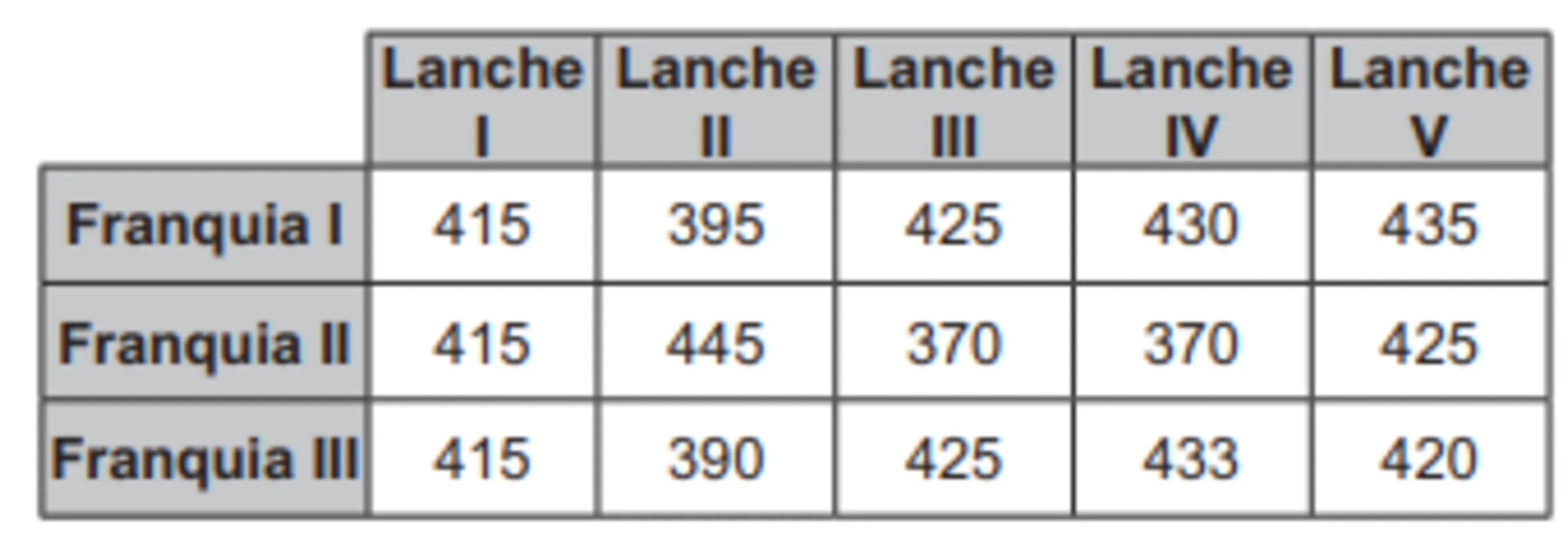
Com base nessas informações, a gerência decidiu incluir no cardápio o lanche de tipo

a) I.

b) II.

c) III.

d) IV.

e) V

08. (ENEM)

Um nutricionista verificou, na dieta diária do seu cliente, a falta de 800 mg do mineral A, de 1 000 mg do mineral B e de 1 200 mg do mineral C. Por isso, recomendou a compra de suplementos alimentares que forneçam os minerais faltantes e informou que não haveria problema se consumisse mais desses minerais do que o recomendado.

O cliente encontrou cinco suplementos, vendidos em sachês unitários, cujos preços e as quantidades dos minerais estão apresentados a seguir:

• Suplemento I: contém 50 mg do mineral A, 100 mg do mineral B e 200 mg do mineral C e custa R$ 2,00;

• Suplemento II: contém 800 mg do mineral A, 250 mg do mineral B e 200 mg do mineral C e custa R$ 3,00;

• Suplemento III: contém 250 mg do mineral A, 1 000 mg do mineral B e 300 mg do mineral C e custa R$ 5,00;

• Suplemento IV: contém 600 mg do mineral A, 500 mg do mineral B e 1 000 mg do mineral C e custa R$ 6,00;

• Suplemento V: contém 400 mg do mineral A, 800 mg do mineral B e 1 200 mg do mineral C e custa R$ 8,00.

O cliente decidiu comprar sachês de um único suplemento no qual gastasse menos dinheiro e ainda suprisse a falta de minerais indicada pelo nutricionista, mesmo que consumisse alguns deles além de sua necessidade.

Nessas condições, o cliente deverá comprar sachês do suplemento

a) I.

b) II.

c) III.

d) IV

e) V.

09. (ENEM)

Aplicativos que gerenciam serviços de hospedagem têm ganhado espaço no Brasil e no mundo por oferecer opções diferenciadas em termos de localização e valores de hospedagem. Em um desses aplicativos, o preço P a ser pago pela hospedagem é calculado considerando um preço por diária d, acrescido de uma taxa fixa de limpeza L e de uma taxa de serviço. Essa taxa de serviço é um valor percentual s calculado sobre o valor pago pelo total das diárias.

Nessa situação, o preço a ser pago ao aplicativo para uma hospedagem de n diárias pode ser obtido pela expressão

a) P =d · n + L + d · n · s

b) P =d · n + L + d · s

c) P =d + L + s

d) P =d · n · s + L

e) P =d · n · L + s

10. (ENEM)

O gráfico apresenta o nível de ocupação dos cinco reservatórios de água que abasteciam uma cidade em 2 de fevereiro de 2015.

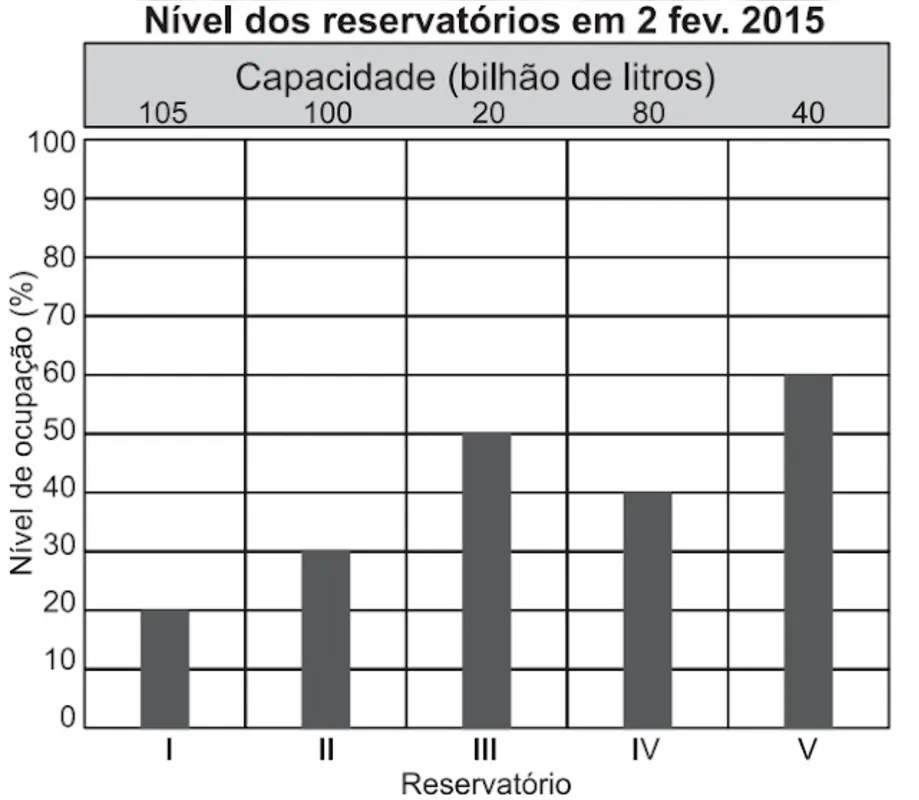
Nessa data, o reservatório com o maior volume de água era o

a) I.

b) II.

c) III.

d) IV

e) V.

11. (ENEM)

Uma unidade de medida comum usada para expressar áreas de terrenos de grandes dimensões é o hectare, que equivale a 10 000 m . Um fazendeiro decide fazer um loteamento utilizando 3 hectares de sua fazenda, dos quais 0,9 hectare será usado para a construção de ruas e calçadas e o restante será dividido em terrenos com área de 300 m cada um. Os 20 primeiros terrenos vendidos terão preços promocionais de R$ 20 000,00 cada, e os demais, R$ 30 000,00 cada.

Nas condições estabelecidas, o valor total, em real, obtido pelo fazendeiro com a venda de todos os terrenos será igual a

a) 700 000.

b) 1 600 000.

c) 1 900.000

d) 2 200 000.

e) 2 800 000.

12. (ENEM)

Um marceneiro visitou 5 madeireiras para comprar tábuas que lhe permitissem construir 5 prateleiras de formato retangular, de dimensões iguais a 30 cm de largura por 120 cm de comprimento cada, tendo como objetivo minimizar a sobra de madeira, podendo, para isso, fazer qualquer tipo de emenda. As dimensões das tábuas encontradas nas madeireiras estão descritas no quadro.

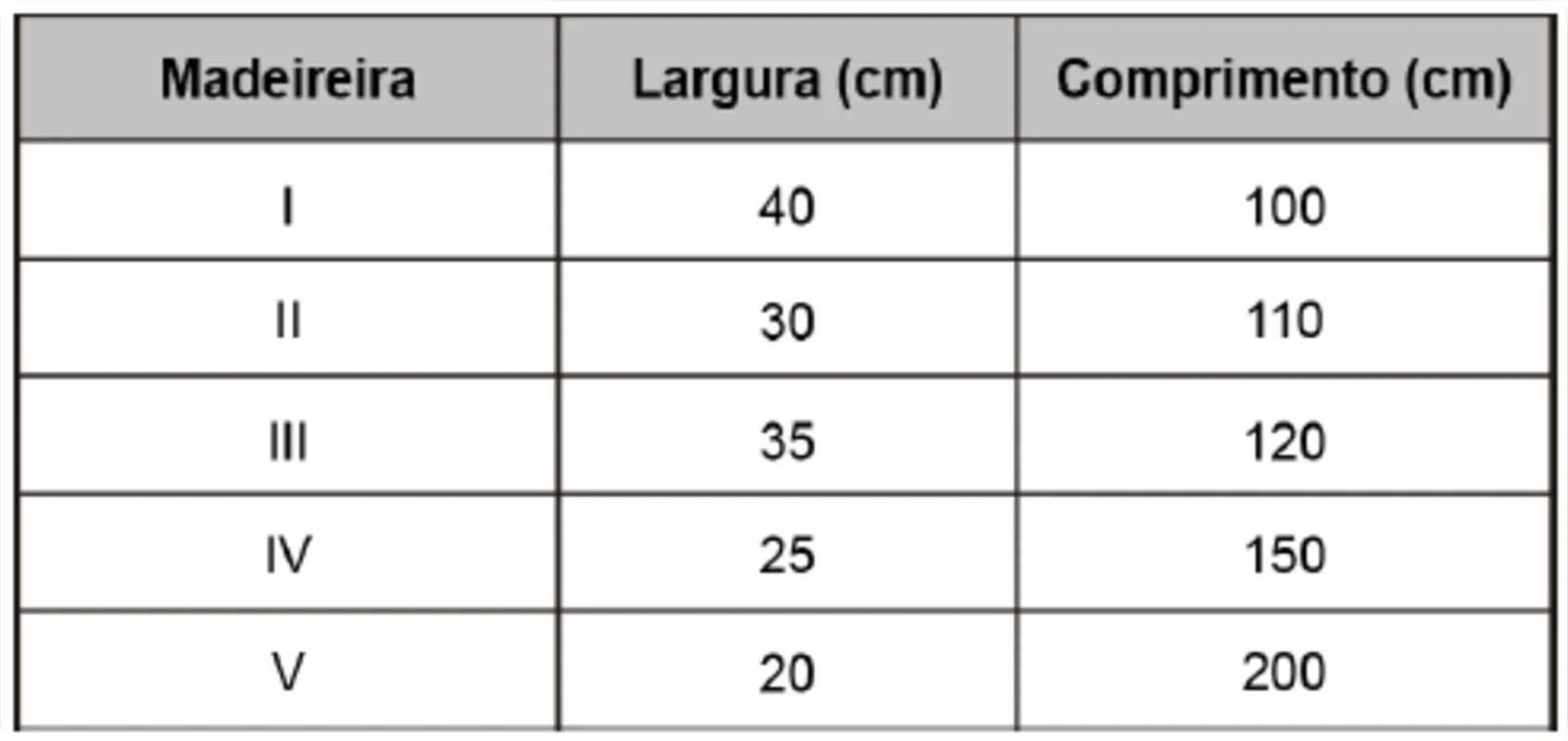
Em qual madeireira o marceneiro deve comprar as tábuas para atingir seu objetivo?

a) I

b) II

c) III

d) IV

e) V

13. (ENEM)

Uma microempresa especializou-se em produzir um tipo de chaveiro personalizado para brindes. O custo de produção de cada unidade é de R$ 0,42 e são comercializados empacotes com 400 chaveiros, que são vendidos por R$ 280,00. Além disso, essa empresa tem um custo mensal fixo de R$ 12 800,00 que não depende do número de chaveiros produzidos.

Qual é o número mínimo de pacotes de chaveiros que devem ser vendidos mensalmente para que essa microempresa não tenha prejuízo no mês?

a) 26

b) 46

c) 109

d) 114

e) 115

14. (ENEM)

Uma empresa de chocolates consultou o gerente de produção e verificou que existem cinco tipos diferentes de barras de chocolate que podem ser produzidas, com os seguintes preços no mercado:

• Barra I: R$ 2,00;

• Barra II: R$ 3,50;

• Barra III: R$ 4,00;

• Barra IV: R$ 7,00;

• Barra V: R$ 8,00.

Analisando as tendências do mercado, que incluem a quantidade vendida e a procura pelos consumidores, o gerente de vendas da empresa verificou que o lucro L com a venda de barras de chocolate é expresso pela função L(x) = – x2 + 14x – 45, em que x representa o preço da barra de chocolate.

A empresa decide investir na fabricação da barra de chocolate cujo preço praticado no mercado renderá o maior lucro.

Nessas condições, a empresa deverá investir na produção da barra

a) I.

b) II.

c) III.

d) IV

e) V.

15. (ENEM)

O gráfico mostra o resultado do balanço financeiro mensal de uma empresa ao longo de um ano.

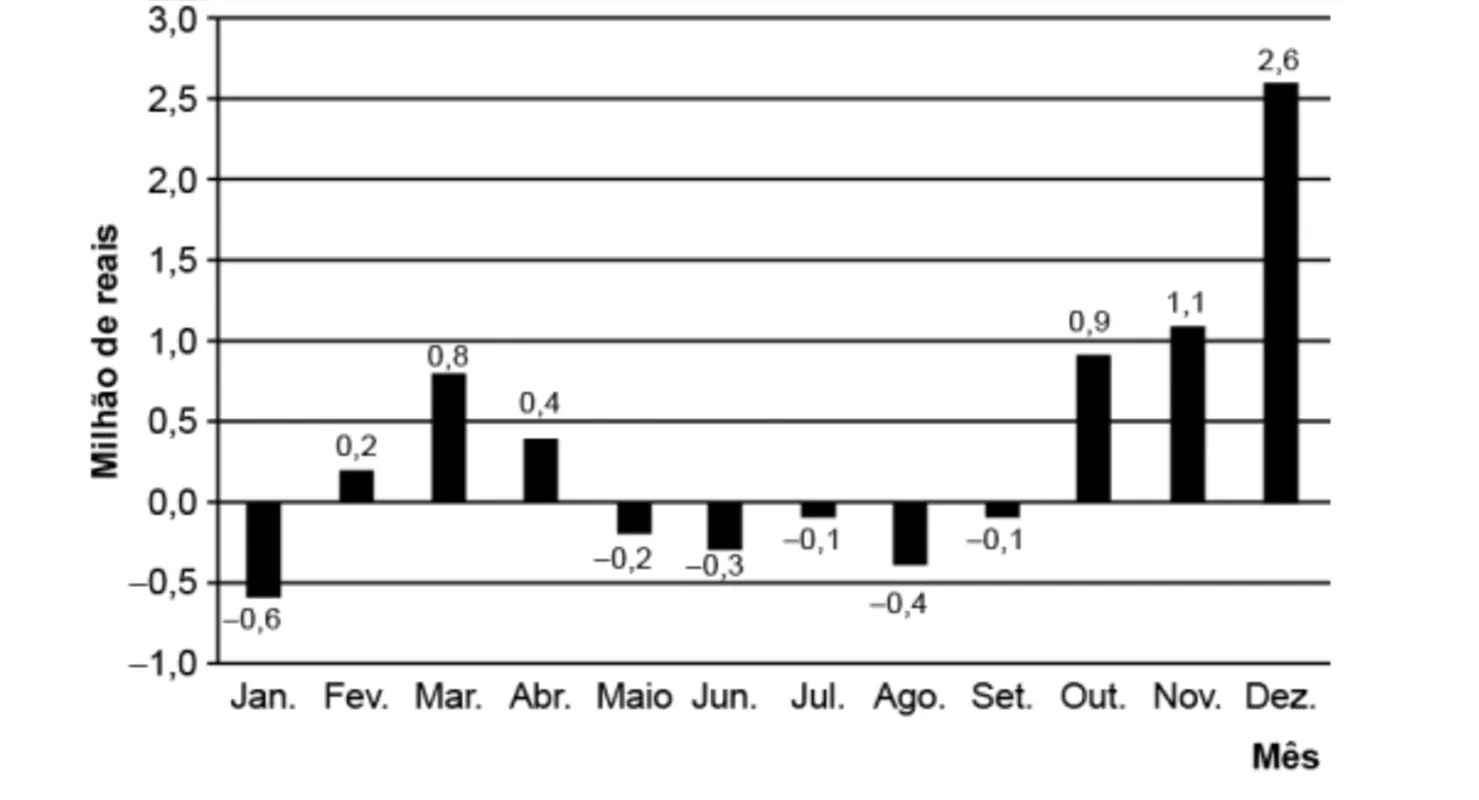
Em quantos meses o resultado do balanço financeiro da empresa ficou abaixo da média mensal nesse ano?

a) 6

b) 7

c) 8

d) 9

e) 10

16. (ENEM)

Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.

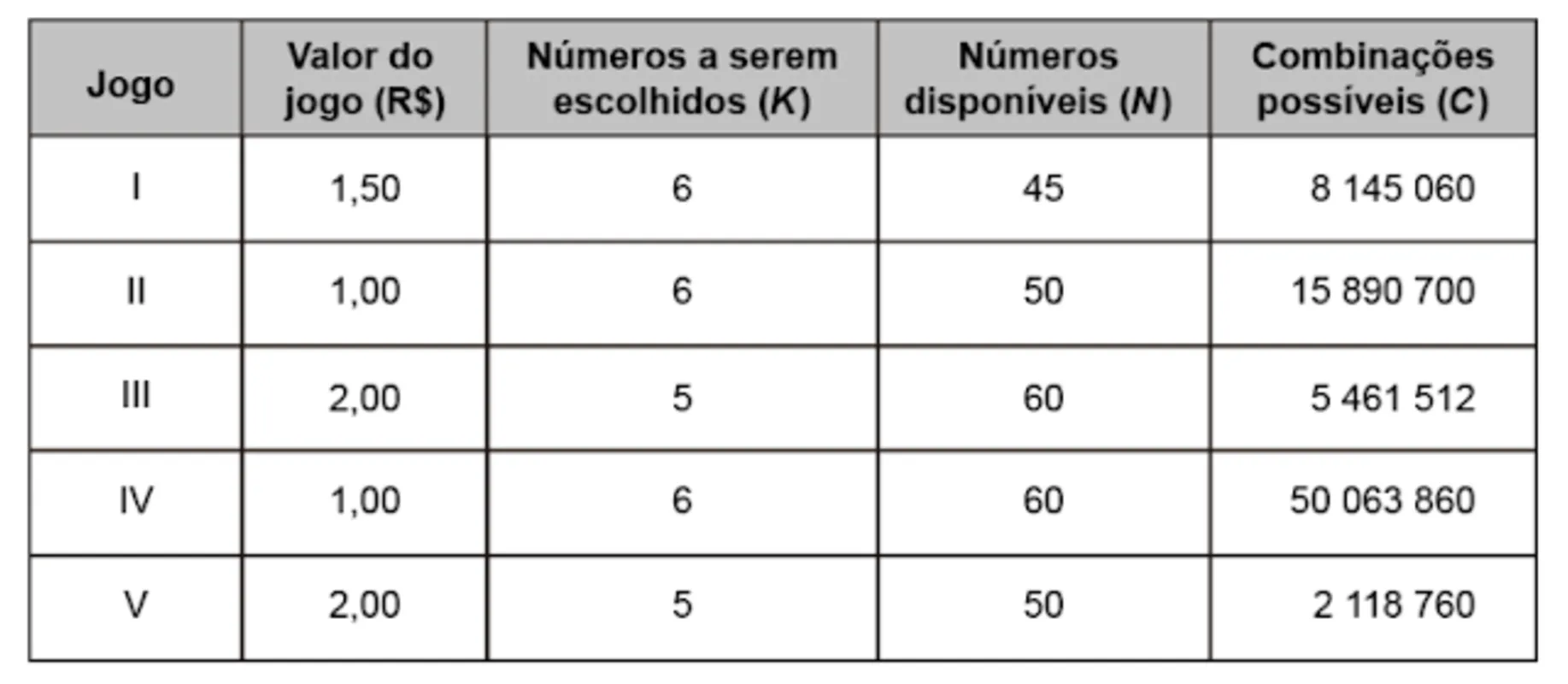
Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.

Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o

a) I.

b) II.

c) III.

d) IV.

e) V

17. (ENEM)

“1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23, GOL, 25, ...”

Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante errava um termo da sequência.

Um dos participantes conseguiu falar até o número 103, respeitando as regras da brincadeira.

O total de vezes em que esse participante disse a palavra GOL foi

a) 20

b) 28

c) 30

d) 35

e) 40

18. (ENEM)

Realizou-se um estudo sobre a violência no Brasil. As taxas obtidas para os homicídios de mulheres de 1980 a 2010 estão registradas no gráfico.

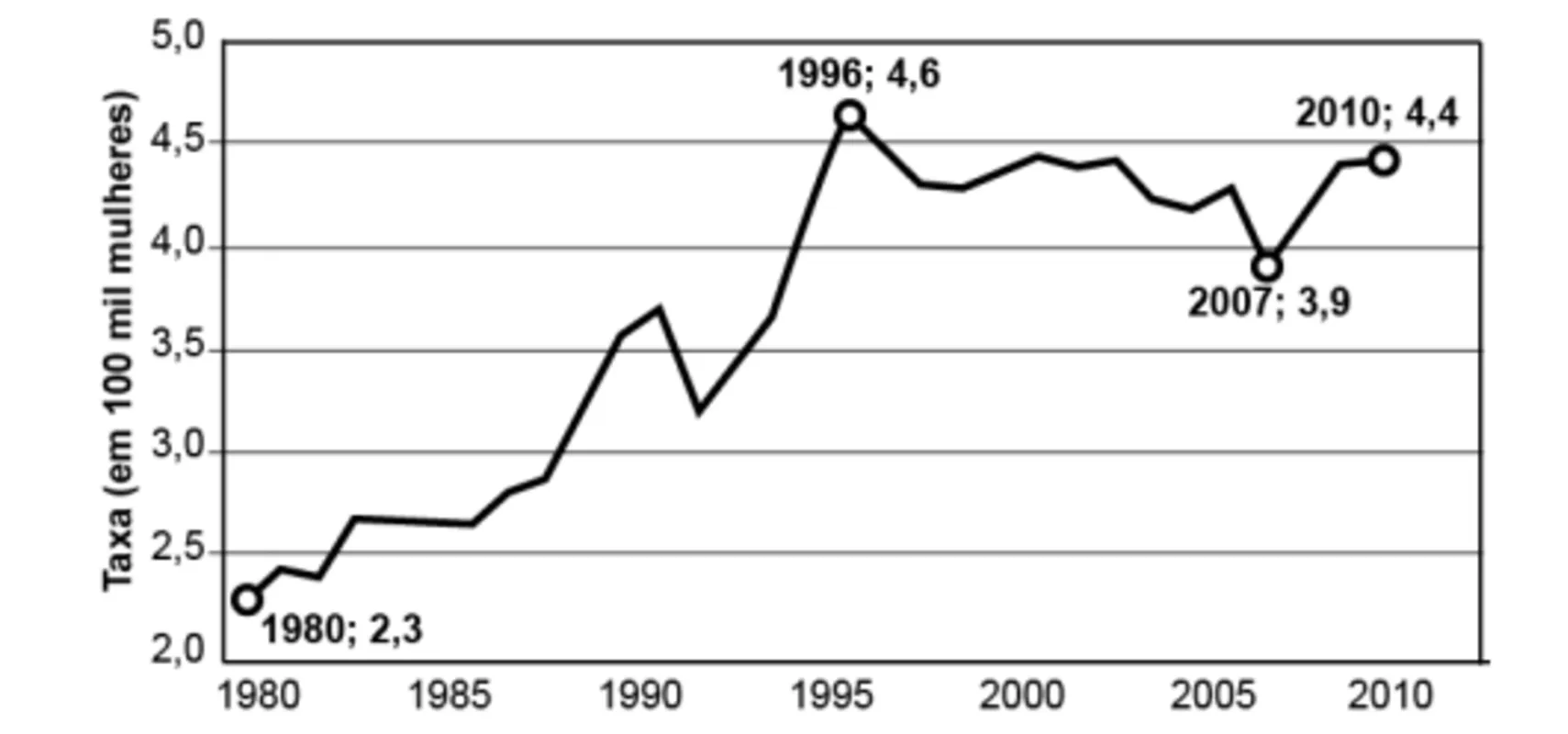
De cordo com os dados apresentados, o aumento percentual relativo da taxa de 2007 para 2010 foi mais próximo de

a) 11%.

b) 13%.

c) 17%.

d) 50%.

e) 89%.

19. (ENEM)

Na última eleição para a presidência de um clube, duas chapas se inscreveram (I e II). Há dois tipos de sócio: patrimoniais e contribuintes. Votos de sócios patrimoniais têm peso 0,6 e de sócios contribuintes têm peso 0,4. A chapa I recebeu 850 votos de sócios patrimoniais e 4300 de sócios contribuintes; a chapa II recebeu 1 300 votos de sócios patrimoniais e 2 120 de sócios contribuintes. Não houve abstenções, votos em branco ou nulos, e a chapa I foi vencedora. Haverá uma nova eleição para a presidência do clube, com o mesmo número e tipos de sócios, e as mesmas chapas da eleição anterior. Uma consulta feita pela chapa II mostrou que os sócios patrimoniais não mudarão seus votos, e que pode contar com os votos dos sócios contribuintes da última eleição. Assim, para que vença, será necessária uma campanha junto aos sócios contribuintes com o objetivo de que mudem seus votos para a chapa II.

A menor quantidade de sócios contribuintes que precisam trocar seu voto da chapa I para a chapa II para que esta seja vencedora é

a) 449.

b) 753

c) 866.

d) 941.

e) 1 091.

CONFIRA O GABARITO COM AS RESPOSTAS DESTE SIMULADO